1.4 正弦波形

在所有波形中，正弦波因其易于表示和一些特定的优势特性而被广泛使用。正弦波或正弦波形是一条描述平滑重复振荡的曲线。

我们可以将正弦波定义为：“波形中，振幅始终与其在每个时间点的位移角度的正弦值成正比”。

什么是正弦波形？

正弦波形的形状像交流电（AC）电路中使用的正弦波。它是一个在正负值之间重复振荡的曲线，表示电压随时间的变化。

所有波形都可以通过叠加正弦波形来生成。正弦波具有重复的模式。这种重复部分的长度称为波长。

正弦波的特性包括：

• 振幅：波形的最大值，从零线到峰值测量。
• 周期：波形完成一个完整周期所需的时间。
• 频率：每秒的周期数，以赫兹（Hz）为单位测量。
• 相位：波形相对于参考点的位置。

正弦波形方程：

其最基本的形式作为时间 $t$ 的函数是

$Y(t) = A \sin(2\pi ft + \varphi) = A \sin(\omega t + \varphi)$

其中：

• $A$ 是振幅，
• $f$ 是频率，
• $\omega = 2\pi f$，角频率，
• $\varphi$ 是相位。

正弦波的形状如下所示：

正弦波形的产生

有许多方法可以生成正弦波形。它们如下所示：

• 石英晶体振荡器
• 负阻振荡器
• 基本单线圈交流发电机
• 相移振荡器
• 文氏桥振荡器等

生成正弦波的基本方法是“基本单线圈发电机”，这在我们之前的文章“交流电理论”中已经解释过。

什么是转速（RPM）？

RPM 代表“每分钟转数”。这意味着“线圈完成的转数”称为“RPM”。例如，如果电机轴在一分钟内完成 100 转，则电机的速度被称为“100 RPM”。

极数总是偶数。

线圈的 RPM、产生的正弦波的频率和极数之间的关系如下：

通常我们说 $\omega = 2\pi f$，但如果旋转是由磁极引起的，我们把角速度写为

$\omega = \frac{2}{n} [2\pi f] \quad \text{其中 } n \text{ 表示极数}$

由于我们知道 $n = 60 f$，则

转数可以写为：

$N_p = \frac{2 \times 60 f}{p}$ $\omega_{\text{转子}} = \frac{2}{\text{极数}} \times 2\pi f \quad (\text{弧度/秒})$ $N_p = \frac{120 f}{\text{极数}} \quad (\text{RPM})$

其中：

• $\omega$ 是正弦波的角速度，
• $N$ 是极数，
• $f$ 是波形的频率，
• $\pi$ 是一个常数，值为 3.1416。

60 Hz 频率机器的极数与速度的关系如下：

50 Hz 频率机器的极数与速度的关系如下：

瞬时电压

瞬时电压是两个点在特定时刻的电压。给定瞬间的波形电压称为“瞬时电压”。

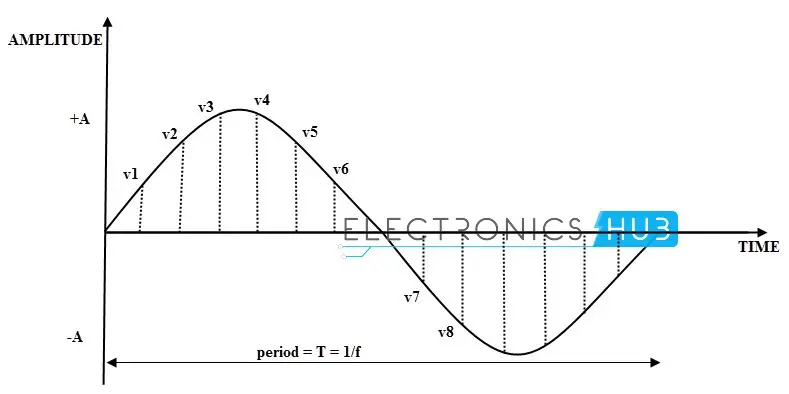
在上图中，$v_1, v_2, v_3, v_4, v_5, v_6 \ldots$ 是正弦波的瞬时电压。

要找到正弦波的瞬时电压值，我们依赖于正弦波的最大电压。

$\text{瞬时电压} = \text{最大电压} \times \sin \theta$ $V_{\text{瞬时}} = V_{\text{最大}} \times \sin \theta$

线圈在磁场中的位移

正弦波的位移由线圈的旋转角度决定。它用 $\theta$ 表示。实际上，为了找到瞬时电压，我们将正弦波的最大或峰-峰电压与线圈旋转角度的正弦值相乘。

线圈在磁场中的旋转角度为：

$\theta = \omega t$

其中：

• $\omega$ 是正弦波的角速度，
• $t$ 是正弦波的时间周期。

对于已知的最大电压值，我们可以沿着波形计算瞬时电压。由于瞬时值给出了正弦波的位置值，我们可以在正弦波上绘制图形。这给出了正弦波的形状。

上图显示了正弦波的振幅。在图（1）中，电枢在磁场中以高振幅移动，因此生成的正弦波将形成正半周期。但在图（2）中，电枢在磁场中以低振幅移动，因此生成的正弦波将形成负半周期。

为了更容易理解这一点，我们将在每个 45° 处绘制正弦波的瞬时值。在一个完整周期内，我们可以为每个 45° 的角度得到 8 个值。

正弦波的构造

通过在磁场中旋转线圈的不同瞬间绘制图形，从 0° 到 360°，我们可以绘制出正弦波的模式。在其中，当正弦波的相位为 0°、180° 和 360° 时，正弦波的振幅为 0，这意味着旋转线圈中没有感应电动势（EMF）。

这是因为移动线圈的任何部分都没有受到磁通线的影响。在位置 A 和 E 处感应的 EMF 为零。同样，在 90° 和 270° 的相位处，正弦波将具有最大振幅。这发生在位置 C 和 G。

在正弦波的其他位置（B、D、F、H），EMF 将根据公式 $e = V_{\text{最大}} \times \sin \theta$ 计算。

移动线圈的相位角与正弦波的电动势（EMF）值的关系如下。

因此，正弦波在 90° 处具有高振幅（正），在 270° 处具有高振幅值（负）。

正弦波的角速度

这是角位移相对于时间的变化率。“角速度”是测量物体在一段时间内角位置变化速率的量。它用 $\omega$ 表示。

它是一个矢量量。角速度的单位：弧度或度

$\omega = 2\pi f \quad (\text{弧度/秒})$

由于印度的交流电频率为 50 Hz，角速度可以测量为 314.16 弧度/秒。角速度定义为交流电发电机中线圈的圆周运动速度。

正如我们已经解释的那样，它用 $\omega$ 表示。它是正弦波周期的函数，即完成一次旋转（T）所需的时间。

我们知道频率与正弦波的周期成反比，即 $f = \frac{1}{T}$。因此，正弦波的角速度与周期的关系为：

$\omega = \frac{2\pi}{T} \quad (\text{弧度/秒})$

从上述公式可以看出，正弦波的角速度与正弦波的周期成反比。这意味着周期值越大，角速度越小，反之亦然。

正弦波形示例

如果一个正弦波定义为 $V_m = 150 \sin(220t)$，那么求其有效值（RMS）、频率以及在 5 毫秒后波形的瞬时值。

解：

正弦波的一般方程为 $V_t = V_m \sin(\omega t)$。

将此方程与给定方程 $V_m = 150 \sin(220t)$ 进行比较：

• 最大电压（峰值）为 150 伏特，
• 角频率为 220 弧度/秒。

波形的有效值（RMS）为：

$V_{\text{RMS}} = 0.707 \times \text{最大振幅或峰值}$ $= 0.707 \times 150 = 106.05 \, \text{伏特}$

正弦波的角度是其频率的函数。由于已知正弦波的角速度，因此可以确定波形的频率。通过 $\omega$ 和 $f$ 之间的关系：

角速度 $\omega$：

频率 $f$：

$f = \frac{\omega}{2\pi}$

对于给定的正弦波形，$\omega = 220$：

$f = \frac{220}{2\pi} = \frac{220}{2 \times 3.1416} = \frac{220}{6.2832} = 35.0140 \, \text{赫兹}$

在 5 毫秒后，瞬时值可以通过以下公式计算：

$V_i = 150 \sin(220 \times 5 \, \text{ms}) = 150 \sin(1.1) = 150 \times 0.8912 = 133.68 \, \text{伏特}$

在 $t = 5 \, \text{ms}$ 时，角度的相位以弧度为单位计算。我们可以非常简单地将弧度值转换为度数。弧度转换为度数的公式为：

$\text{度数} = \left(\frac{180}{\pi}\right) \times \text{弧度}$

将 1.1 弧度转换为度数：

$\text{度数} = \left(\frac{180}{\pi}\right) \times 1.1 = 63.02 \, \text{度}$

交流电路与正弦波

正弦波是交流电路中使用的基本波形。当一个正弦电压施加到电路时，它会导致正弦电流流动。电压和电流之间的关系取决于电路中的元件（电阻、电容、电感）。

正弦波在交流电路中的行为取决于以下元件：

• 电阻：在纯电阻电路中，电流和电压同相。
• 电容：在纯电容电路中，电流比电压超前 90 度。
• 电感：在纯电感电路中，电流比电压滞后 90 度。

结论：

正弦波形是交流电路的基石。它们的特性，包括振幅、周期、频率和相位，是理解交流系统中电气元件行为的基础。电压和电流之间的相互作用，以相位关系为特征，对电路性能有显著影响。通过掌握这些概念，工程师和技术人员可以有效地分析、设计和排除交流电路的故障，优化电力输送和系统效率。

对正弦波形及其在交流电路中的相互作用的深入理解，对于从电力生成和传输到电子和通信系统等各种应用都是必不可少的。